One Layer of CNN

Now let’s implement a single step of convolution, in which you apply the filter to a single position of the input. This will be used to build a convolutional unit, which:

  • Takes an input volume
  • Applies a filter at every position of the input
  • Outputs another volume (usually of different size)

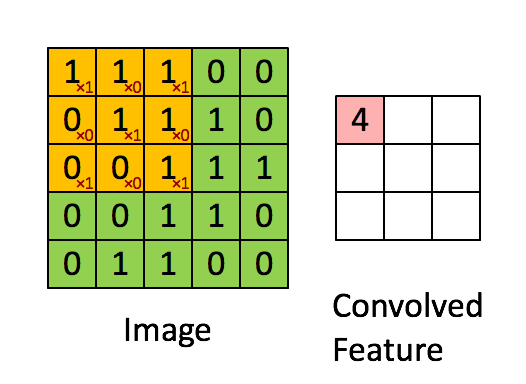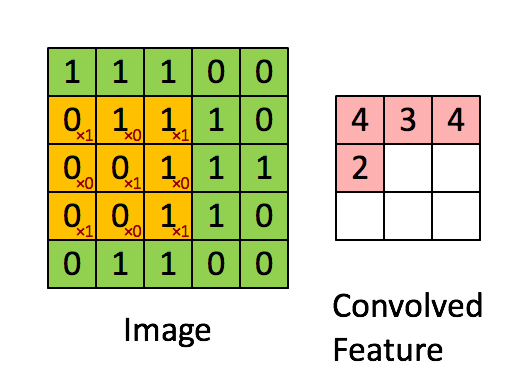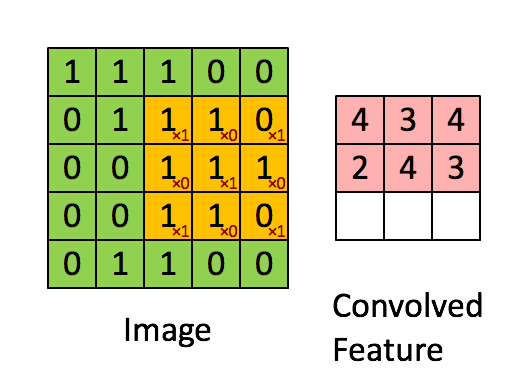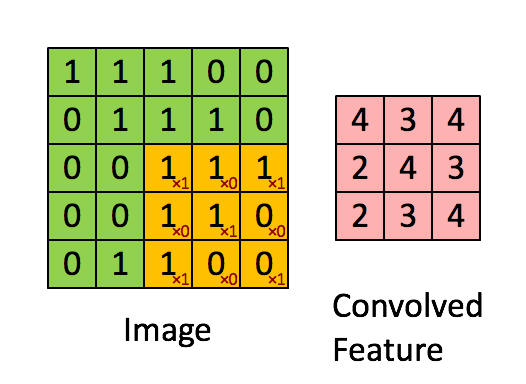
As a recap:

In a computer vision application, each value in the matrix on the left corresponds to a single pixel value, and we convolve a 3x3 filter with the image by multiplying its values element-wise with the original matrix, then summing them up and adding a bias. In this first step of the exercise, you will implement a single step of convolution, corresponding to applying a filter to just one of the positions to get a single real-valued output.

One Convolution Layer

We will later cover how to apply this function to multiple positions of the input to demonstrate the full convolutional operation.

Going back to the multidimensional example from the last page and add a bias which is a real number that’s constant for the entire branch of the layer.

  • Let’s say we have an image that’s 1000x1000x3 and we have 10 filters: 3x3x3, how many parameters do we have?
  • Remember that the parameters w1 … w9 for each filter and each filter has 3 channels, so each filter will have 9x3=27 parameters
  • Plus we will have one bias for each filter, so in order to complete the 1 layer network we have the w parameters and b (the bias) so we have a total of 28 parameters/filter
  • Since we have 10 filters, the total number of parameters will be 280 regardless of how large the input image is

So here is how to summarize the notations of 1 layer of convolution:

  • Superscript [l] denotes an object of the lth layer.

    • Example: a[4] is the 4th layer activation. W[5] and b[5] are the 5th layer parameters.

  • Superscript (i) denotes an object from the ith example.

    • Example: x(i) is the ith training example input.

  • Lowerscript i denotes the ith entry of a vector.

    • Example: ai[l] denotes the ith entry of the activations in layer l, assuming this is a fully connected (FC) layer.

  • nH, nW and nC denote respectively the height, width and number of channels of a given layer. If you want to reference a specific layer l, you can also write nH[l], nW[l], nC[l].

  • nHprev, nWprev and nCprev denote respectively the height, width and number of channels of the previous layer. If referencing a specific layer l, this could also be denoted nH[l−1], nW[l−1],

Example

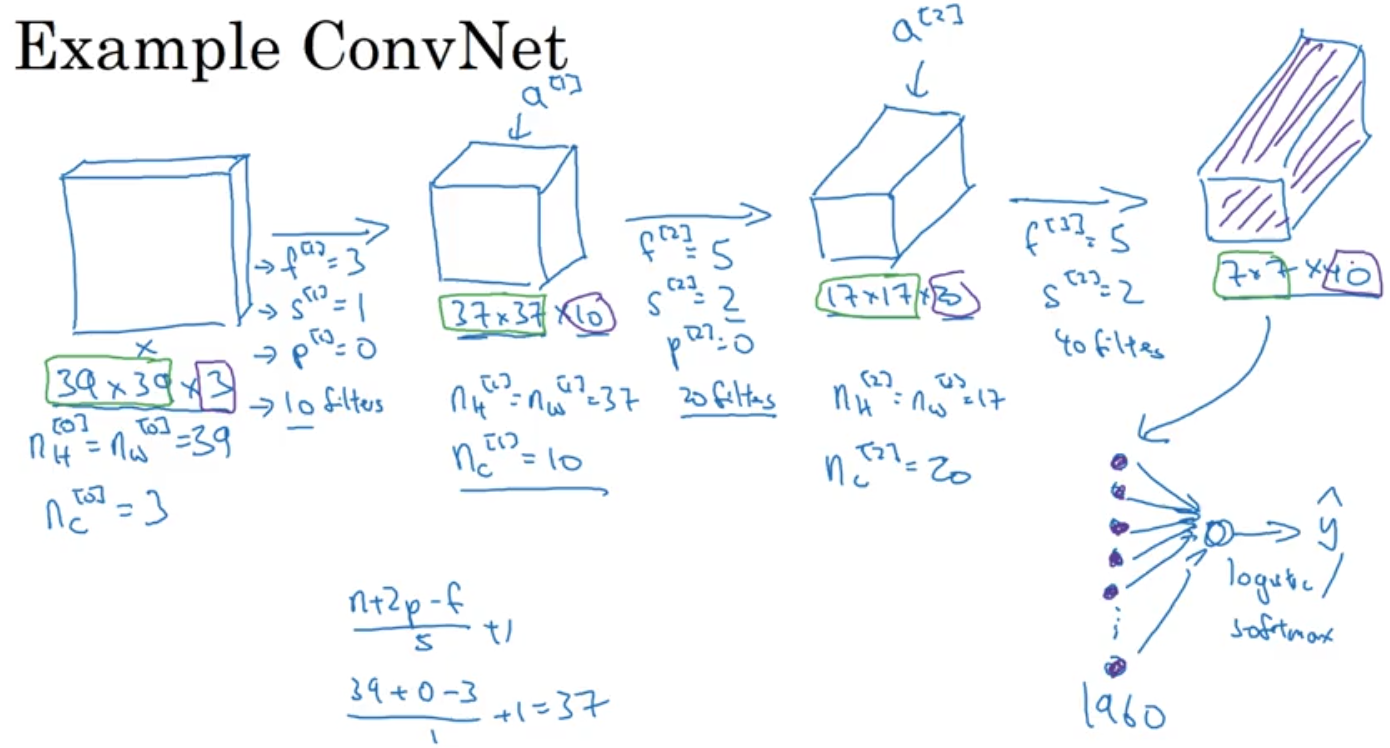
Let’s look at an example of a single convolutional layer network ConvNet:

  • Input 39x39x3 (3 (channels) -> 37x37x10 ->17x17x20 -> 7x7x40
  • 10 filters in first layer, 20 filters in second layer, 40 filters in last layer
  • First Layer: 3x3 filters, Stride=1, Padding =0… as shown below
  • As you see below we’ve taken an input of 39x39x3 and ended up with an output of 7x7x40 cube of Features
  • Then we take the output of Features and Flatten it into (7x7x40=1960 ) units vector and feed it into a logistic regression function or Softmax logistic regression to get the output \(\hat{y}\)

So we just saw an example of a ConvNet (convolutional network layer), even though that could suffice in being a complete NN, it is more efficient to have other layers to improve effectiveness and efficiency, those layers are

  • Convolution
  • Pooling
  • Fully connected (FC)

We will cover them in the next pages. For now let’s look at the code involved in a one layer ConvNet

Code

Let’s start with:

  • Input: 4x4x3
  • Parameters w = (4,4,3)
  • Bias b = (1,1,1)
  • Let’s calculate Z (in the above example this value was \(\hat{y}\) )
def conv_single_step(a_slice_prev, W, b):
    """
    Apply one filter defined by parameters W on a single slice (a_slice_prev) of the output activation 
    of the previous layer.
    
    Arguments:
    a_slice_prev -- slice of input data of shape (f, f, n_C_prev)
    W -- Weight parameters contained in a window - matrix of shape (f, f, n_C_prev)
    b -- Bias parameters contained in a window - matrix of shape (1, 1, 1)
    
    Returns:
    Z -- a scalar value, result of convolving the sliding window (W, b) on a slice x of the input data
    """

    # Element-wise product between a_slice and W. Do not add the bias yet.
    s = np.multiply(a_slice_prev,W)
    # Sum over all entries of the volume s.
    Z = np.sum(s)
    # Add bias b to Z. Cast b to a float() so that Z results in a scalar value.
    Z = Z + np.asarray(b, dtype=float)
    return Z
np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)

Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)
Z = [[[-6.99908945]]]

Example

  • Implement a function that takes as input A_prev, the activations output by the previous layer (from a batch of m inputs)
  • F filters/weights denoted by W
  • Bias vector denoted by b, where each filter has its own single bias.
  • Access the hyperparameters dictionary which contains the stride and the padding
  • To select a slice of 2x2 at the upper left corner of a matrix a_prev of shape(5,3) we would use a_slice_prev = a_prev[0:2,0:2,:]
  • We will not worry about vector calculations for this example

This will be useful when you will define a_slice_prev below, using the start/end indexes you will define. 2. To define a_slice you will need to first define its corners vert_start, vert_end, horiz_start and horiz_end. This figure may be helpful for you to find how each of the corner can be defined using h, w, f and s in the code below.

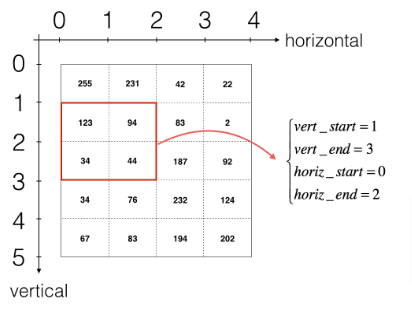
  • Reminder: the formulas are

def conv_forward(A_prev, W, b, hparameters):
    """
    Implements the forward propagation for a convolution function
    
    Arguments:
    A_prev -- output activations of the previous layer, numpy array of shape (m, n_H_prev, n_W_prev, n_C_prev)
    W -- Weights, numpy array of shape (f, f, n_C_prev, n_C)
    b -- Biases, numpy array of shape (1, 1, 1, n_C)
    hparameters -- python dictionary containing "stride" and "pad"
        
    Returns:
    Z -- conv output, numpy array of shape (m, n_H, n_W, n_C)
    cache -- cache of values needed for the conv_backward() function
    """
    
    ### START CODE HERE ###
    # Retrieve dimensions from A_prev's shape (≈1 line)  
    (m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
    
    # Retrieve dimensions from W's shape (≈1 line)
    (f, f, n_C_prev, n_C) = W.shape
    
    # Retrieve information from "hparameters" (≈2 lines)
    stride = hparameters["stride"]
    padding = hparameters["pad"]
    
    # Compute the dimensions of the CONV output volume using the formula given above. Hint: use int() to floor. (≈2 lines)
    n_H = int(((n_H_prev + (2*padding) - f)/stride + 1))
    n_W = int(((n_W_prev + (2*padding) - f)/stride + 1))
    
    # Initialize the output volume Z with zeros. (≈1 line)
    Z = np.zeros((m,n_H,n_W,n_C))
    
    # Create A_prev_pad by padding A_prev
    A_prev_pad = zero_pad(A_prev,padding)
    
    for i in range(0,m):                               # loop over the batch of training examples
        a_prev_pad = A_prev_pad[i]                               # Select ith training example's padded activation
        for h in range(0,n_H):                           # loop over vertical axis of the output volume
            for w in range(0,n_W):                       # loop over horizontal axis of the output volume
                for c in range(0,n_C):                   # loop over channels (= #filters) of the output volume
                    
                    # Find the corners of the current "slice" (≈4 lines)
                    vert_start = h*stride
                    vert_end = vert_start + f
                    horiz_start = w*stride
                    horiz_end = horiz_start + f
                    
                    # Use the corners to define the (3D) slice of a_prev_pad (See Hint above the cell). (≈1 line)
                    a_slice_prev = a_prev_pad[vert_start:vert_end,horiz_start:horiz_end,:]
                    # Convolve the (3D) slice with the correct filter W and bias b, to get back one output neuron. (≈1 line)
                    Z[i, h, w, c] = conv_single_step(a_slice_prev,W[:,:,:,c],b[:,:,:,c])
                                        
    ### END CODE HERE ###
    
    # Making sure your output shape is correct
    assert(Z.shape == (m, n_H, n_W, n_C))
    
    # Save information in "cache" for the backprop
    cache = (A_prev, W, b, hparameters)
    
    return Z, cache
np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
               "stride": 2}

Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =", np.mean(Z))
print("Z[3,2,1] =", Z[3,2,1])
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])