a = np.random.randn(19*19, 5, 1)
b = np.random.randn(19*19, 5, 80)
c = a * b # shape of c will be (19*19, 5, 80)
# So our box scores will be
box_scores = box_confidence * box_class_probsVisualize Classes
OD Basics Code Examples
This page is a recap of most of the definitions we’ve learned about OD but shown in example codes.
Case Study
- We will guild a car detection system
- To collect data, we’re using a dash mounted camera which takes pictures of the road ahead every few seconds
- We’ve gathered all these images into a folder and have labeled them by drawing bounding boxes around every car
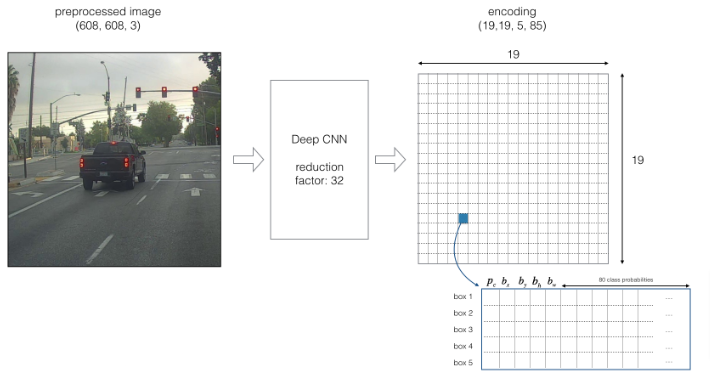
- Input image (608, 608, 3)
- The input image goes through a CNN, resulting in a (19,19,5,85) dimensional output.
- After flattening the last two dimensions, the output is a volume of shape (19, 19, 425):
- Each cell in a 19x19 grid over the input image gives 425 numbers.
- 425 = 5 x 85 because each cell contains predictions for 5 boxes, corresponding to 5 anchor boxes, as seen in lecture.
- 85 = 5 + 80 where 5 is because (pc,bx,by,bh,bw) has 5 numbers, and 80 is the number of classes we’d like to detect
- You then select only few boxes based on:
- Score-thresholding: throw away boxes that have detected a class with a score less than the threshold
- Non-max suppression: Compute the Intersection over Union and avoid selecting overlapping boxes
- This gives you YOLO’s final output.
Bounding Boxes
Here are the details of the bounding boxes:
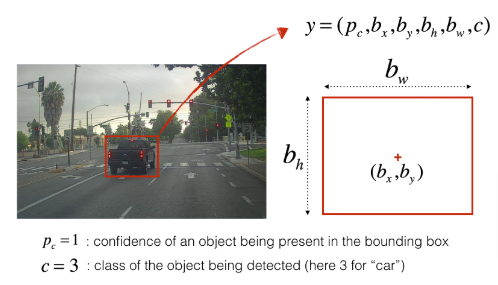
- As we covered before, we can represent all the classes (let’s say 80) in label c which is an integer from 1 to 80
- Or we can represent them as an 80 dimensional vector with one component which is 1 for the class detected and the rest being 0
We will use a Yolo model which has been pre-trained which means instead of training the model and retrieving the weights, we will be using the provided weights since we will be using a pre-trained model.
YOLO
“You Only Look Once” (YOLO) is a popular algorithm because it achieves high accuracy while also being able to run in real-time. This algorithm “only looks once” at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
Model Details
Inputs and outputs
- The input is a batch of images, and each image has the shape (m, 608, 608, 3)
- The output is a list of bounding boxes along with the recognized classes. Each bounding box is represented by 6 numbers (pc,bx,by,bh,bw,c) as explained above. If you expand c into an 80-dimensional vector, each bounding box is then represented by 85 numbers.
Anchor Boxes
- Anchor boxes are chosen by exploring the training data to choose reasonable height/width ratios that represent the different classes. For this assignment, 5 anchor boxes were chosen for you (to cover the 80 classes), and stored in the file ‘./model_data/yolo_anchors.txt’
- The dimension for anchor boxes is the second to last dimension in the encoding: (m,nH,nW,anchors,classes).
- The YOLO architecture is: IMAGE (m, 608, 608, 3) -> DEEP CNN -> ENCODING (m, 19, 19, 5, 85).
Encoding
Let’s look in greater detail at what this encoding represents. Remember if the center/midpoint of an object that was detected falls into a grid cell, that grid cell will be marked for detecting that object.
- We will be using 19x19 grid for encoding
Since we are using 5 anchor boxes, each of the 19 x19 cells thus encodes information about 5 boxes. Anchor boxes are defined only by their width and height.
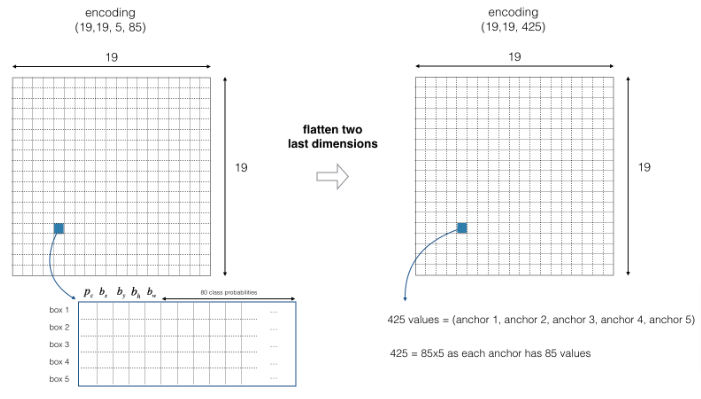
Flatten Output
For simplicity, we will flatten the last two last dimensions of the shape (19, 19, 5, 85) encoding. So the output of the Deep CNN is (19, 19, 425).
Class Score
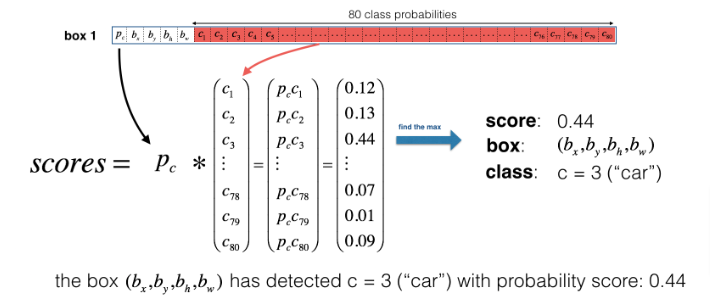
- For each grid cell, we will compute the probability that the grid cell contains a class and we name that
- scorec,i = pc X ci which is calculated by multiplying the probability that there is an object of a certain class
- In figure below, let’s say for box 1 (cell 1), the probability that an object exists is p1=0.60. So there’s a 60% chance that an object exists in box 1 (cell 1).
- The probability that the object is the class “category 3 (a car)” is c3=0.73.
- The score for box 1 and for category “3” is score1,3=0.60×0.73=0.44.
- Let’s say we calculate the score for all 80 classes in box 1, and find that the score for the car class (class 3) is the maximum. So we’ll assign the score 0.44 and class “3” to this box “1”.
Code
- To compute the box scores we need to multiply the probability an object exists in the box with the probability the object is of class
- We could use broadcasting (which is multiplying vectors of different sizes) to get our results like this
- The variables are described down below in Filter by Threshold section
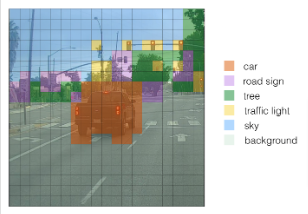
We can visualize what YOLO is predicting on an image by
- For each of the 19x19 grid cells, find the maximum of the probability scores (taking a max across the 80 classes, one maximum for each of the 5 anchor boxes).
- Color that grid cell according to what object that grid cell considers the most likely.
- Or we can plot all the Bounding Boxes at once and we get

Non-Max Suppression
- The image above is a plot of the boxes the model assigned a high probability to, we can filter is further by
- Use non-max suppression which
- gets rid of boxes with a low score which means it is either not confident about detecting a class either due to the low probability of any object being in it, or a low probability of this particular class
- selects only one box when many overlap while detecting the same object
Code
- Now that we have the box scores we
- Need to find the maximum box score for each box and extract the index of the class for that max box score
- We also need to extract the corresponding maximum box score
box_classes = K.argmax(box_scores, axis = -1)
box_class_scores = K.max(box_scores, axis = -1, keepdims=False)
# second part could be done this way as well
# box_class_scores = tf.math.reduce_max(box_scores, axis=-1, keepdims=False)Keras argmax
For the axis parameter of argmax and max, if you want to select the last axis, one way to do so is to set axis=-1. This is similar to Python array indexing, where you can select the last position of an array using arrayname[-1]. * Applying max normally collapses the axis for which the maximum is applied. keepdims=False is the default option, and allows that dimension to be removed. We don’t need to keep the last dimension after applying the maximum here. * Even though the documentation shows keras.backend.argmax, use keras.argmax. Similarly, use keras.max.
Filter by Threshold
We will now filter out any boxes that don’t meet the class “score” threshold we choose.
- The model gives you a total of 19x19x5x85 numbers, with each box described by 85 numbers. It is convenient to rearrange the (19,19,5,85) (or (19,19,425)) dimensional tensor into the following variables:
box_confidence: tensor of shape (19×19,5,1) containing pc (confidence probability that there’s some object) for each of the 5 boxes predicted in each of the 19x19 cells.boxes: tensor of shape (19×19,5,4) containing the midpoint and dimensions (bx,by,bh,bw) for each of the 5 boxes in each cell.box_class_probs: tensor of shape (19×19,5,80) containing the “class probabilities” (c1,c2,…c80) for each of the 80 classes for each of the 5 boxes per cell.
Code
- We can filter via threshold by creating a mask
- As a reminder:
([0.9, 0.3, 0.4, 0.5, 0.1] < 0.4)returns:[False, True, False, False, True]. The mask should be True for the boxes we want to keep. - Use TensorFlow to apply the mask to
box_class_scores,boxesandbox_classesto filter out the boxes we don’t want. - We will be left with just the subset of boxes we want to keep.
- We can use
tf.boolean_maskand keep the defaultaxis=None
filtering_mask = (box_class_scores >= threshold)
scores = tf.boolean_mask(box_class_scores, filtering_mask)
boxes = tf.boolean_mask(boxes, filtering_mask)
classes = tf.boolean_mask(box_classes, filtering_mask)Code
Packages
import argparse
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
import scipy.io
import scipy.misc
import numpy as np
import pandas as pd
import PIL
import tensorflow as tf
from keras import backend as K
from keras.layers import Input, Lambda, Conv2D
from keras.models import load_model, Model
from yolo_utils import read_classes, read_anchors, generate_colors, preprocess_image, draw_boxes, scale_boxes
from yad2k.models.keras_yolo import yolo_head, yolo_boxes_to_corners, preprocess_true_boxes, yolo_loss, yolo_body
%matplotlib inlineBoxes & Threshold
Let’s combine the code chunks above together to get:
def yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = .6):
"""Filters YOLO boxes by thresholding on object and class confidence.
Arguments:
box_confidence -- tensor of shape (19, 19, 5, 1)
boxes -- tensor of shape (19, 19, 5, 4)
box_class_probs -- tensor of shape (19, 19, 5, 80)
threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
Returns:
scores -- tensor of shape (None,), containing the class probability score for selected boxes
boxes -- tensor of shape (None, 4), containing (b_x, b_y, b_h, b_w) coordinates of selected boxes
classes -- tensor of shape (None,), containing the index of the class detected by the selected boxes
Note: "None" is here because you don't know the exact number of selected boxes, as it depends on the threshold.
For example, the actual output size of scores would be (10,) if there are 10 boxes.
"""
# Step 1: Compute box scores
box_scores = box_confidence * box_class_probs
# Step 2: Find the box_classes using the max box_scores, keep track of the corresponding score
box_classes = K.argmax(box_scores, axis = -1)
box_class_scores = K.max(box_scores, axis = -1, keepdims=False)
# Step 3: Create a filtering mask based on "box_class_scores" by using "threshold". The mask should have the
# same dimension as box_class_scores, and be True for the boxes you want to keep (with probability >= threshold)
filtering_mask = (box_class_scores >= threshold)
# Step 4: Apply the mask to box_class_scores, boxes and box_classes
scores = tf.boolean_mask(box_class_scores, filtering_mask)
boxes = tf.boolean_mask(boxes, filtering_mask)
classes = tf.boolean_mask(box_classes, filtering_mask)
return scores, boxes, classesNote In yolo_filter_boxes, we’re using random numbers to test the function. In real data, the box_class_probs would contain non-zero values between 0 and 1 for the probabilities. The box coordinates in boxes would also be chosen so that lengths and heights are non-negative.
with tf.Session() as test_a:
box_confidence = tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([19, 19, 5, 4], mean=1, stddev=4, seed = 1)
box_class_probs = tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = 0.5)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.shape))
print("boxes.shape = " + str(boxes.shape))
print("classes.shape = " + str(classes.shape))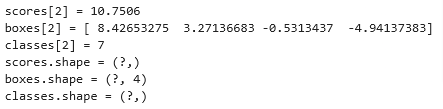
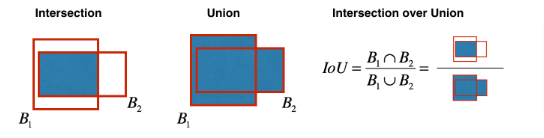
IoU
We did process a non-max suppression earlier above but let’s do this. Even after filtering by threshold over the class scores, we still end up with a lot of overlapping boxes. Instead of choosing the maximum scores let’s calculate the IoU
- In this code, we use the convention that (0,0) is the top-left corner of an image, (1,0) is the upper-right corner, and (1,1) is the lower-right corner. In other words, the (0,0) origin starts at the top left corner of the image. As x increases, we move to the right. As y increases, we move down.
- We define a box using its two corners: upper left (x1,y1) and lower right (x2,y2), instead of using the midpoint, height and width. (This makes it a bit easier to calculate the intersection).
- To calculate the area of a rectangle, multiply its height (y2−y1) by its width (x2−x1). (Since (x1,y1) is the top left and x2,y2 are the bottom right, these differences should be non-negative.
- To find the intersection of the two boxes (xi1,yi1,xi2,yi2):
Feel free to draw some examples on paper to clarify this conceptually.
The top left corner of the intersection (xi1,yi1) is found by comparing the top left corners (x1,y1) of the two boxes and finding a vertex that has an x-coordinate that is closer to the right, and y-coordinate that is closer to the bottom.
The bottom right corner of the intersection (xi2,yi2) is found by comparing the bottom right corners (x2,y2) of the two boxes and finding a vertex whose x-coordinate is closer to the left, and the y-coordinate that is closer to the top.
The two boxes may have no intersection. You can detect this if the intersection coordinates you calculate end up being the top right and/or bottom left corners of an intersection box. Another way to think of this is if you calculate the height (y2−y1) or width (x2−x1) and find that at least one of these lengths is negative, then there is no intersection (intersection area is zero).
The two boxes may intersect at the edges or vertices, in which case the intersection area is still zero. This happens when either the height or width (or both) of the calculated intersection is zero.
Note:
xi1= maximum of the x1 coordinates of the two boxesyi1= maximum of the y1 coordinates of the two boxesxi2= minimum of the x2 coordinates of the two boxesyi2= minimum of the y2 coordinates of the two boxesinter_area= You can usemax(height, 0)andmax(width, 0)
def iou(box1, box2):
"""Implement the intersection over union (IoU) between box1 and box2
Arguments:
box1 -- first box, list object with coordinates (box1_x1, box1_y1, box1_x2, box_1_y2)
box2 -- second box, list object with coordinates (box2_x1, box2_y1, box2_x2, box2_y2)
"""
# Assign variable names to coordinates for clarity
(box1_x1, box1_y1, box1_x2, box1_y2) = box1
(box2_x1, box2_y1, box2_x2, box2_y2) = box2
# Calculate the (yi1, xi1, yi2, xi2) coordinates of the intersection of box1 and box2. Calculate its Area.
xi1 = np.maximum(box1[0], box2[0])
yi1 = np.maximum(box1[1], box2[1])
xi2 = np.minimum(box1[2], box2[2])
yi2 = np.minimum(box1[3], box2[3])
inter_width = xi2-xi1
inter_height = yi2-yi1
# Case in which they don't intersec --> max(,0)
inter_area = max(inter_width, 0) * max(inter_height, 0)
# Calculate the Union area by using Formula: Union(A,B) = A + B - Inter(A,B)
box1_area = (box1[2]-box1[0])*(box1[3]-box1[1])
box2_area = (box2[2]-box2[0])*(box2[3]-box2[1])
union_area = box1_area + box2_area - inter_area
# compute the IoU
iou = float(inter_area)/float(union_area)
return iouTest
## Test case 1: boxes intersect
box1 = (2, 1, 4, 3)
box2 = (1, 2, 3, 4)
print("iou for intersecting boxes = " + str(iou(box1, box2)))
## Test case 2: boxes do not intersect
box1 = (1,2,3,4)
box2 = (5,6,7,8)
print("iou for non-intersecting boxes = " + str(iou(box1,box2)))
## Test case 3: boxes intersect at vertices only
box1 = (1,1,2,2)
box2 = (2,2,3,3)
print("iou for boxes that only touch at vertices = " + str(iou(box1,box2)))
## Test case 4: boxes intersect at edge only
box1 = (1,1,3,3)
box2 = (2,3,3,4)
print("iou for boxes that only touch at edges = " + str(iou(box1,box2)))
Now let’s implement:
TF Non-Max Suppression
- Select the box that has the highest score.
- Compute the overlap of this box with all other boxes, and remove boxes that overlap significantly (iou >=
iou_threshold). - Go back to step 1 and iterate until there are no more boxes with a lower score than the currently selected box.
- This will remove all boxes that have a large overlap with the selected boxes. Only the “best” boxes remain.
Implement yolo_non_max_suppression() using TensorFlow. TensorFlow has two built-in functions that are used to implement non-max suppression (so you don’t actually need to use your
iou()implementation)
Here are the functions used for reference
tf.image.non_max_suppression(
boxes,
scores,
max_output_size,
iou_threshold=0.5,
name=None
)
keras.gather(
reference,
indices
)def yolo_non_max_suppression(scores, boxes, classes, max_boxes = 10, iou_threshold = 0.5):
"""
Applies Non-max suppression (NMS) to set of boxes
Arguments:
scores -- tensor of shape (None,), output of yolo_filter_boxes()
boxes -- tensor of shape (None, 4), output of yolo_filter_boxes() that have been scaled to the image size (see later)
classes -- tensor of shape (None,), output of yolo_filter_boxes()
max_boxes -- integer, maximum number of predicted boxes you'd like
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (, None), predicted score for each box
boxes -- tensor of shape (4, None), predicted box coordinates
classes -- tensor of shape (, None), predicted class for each box
Note: The "None" dimension of the output tensors has obviously to be less than max_boxes. Note also that this
function will transpose the shapes of scores, boxes, classes. This is made for convenience.
"""
max_boxes_tensor = K.variable(max_boxes, dtype='int32') # tensor to be used in tf.image.non_max_suppression()
K.get_session().run(tf.variables_initializer([max_boxes_tensor])) # initialize variable max_boxes_tensor
# Use tf.image.non_max_suppression() to get the list of indices corresponding to boxes you keep
nms_indices = tf.image.non_max_suppression(boxes, scores, max_output_size=max_boxes, iou_threshold=iou_threshold)
# Use K.gather() to select only nms_indices from scores, boxes and classes
scores = K.gather(scores, nms_indices)
boxes = K.gather(boxes, nms_indices)
classes = K.gather(classes, nms_indices)
return scores, boxes, classes# Test
with tf.Session() as test_b:
scores = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([54, 4], mean=1, stddev=4, seed = 1)
classes = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
Filter
Let’s implement yolo_eval() which takes the output of the YOLO encoding and filters the boxes using score threshold and NMS. There’s just one last implementational detail you have to know. There’re a few ways of representing boxes, such as via their corners or via their midpoint and height/width. YOLO converts between a few such formats at different times, using the following functions (which we have provided):
boxes = yolo_boxes_to_corners(box_xy, box_wh)which converts the yolo box coordinates (x,y,w,h) to box corners’ coordinates (x1, y1, x2, y2) to fit the input of yolo_filter_boxes
boxes = scale_boxes(boxes, image_shape)YOLO’s network was trained to run on 608x608 images. If you are testing this data on a different size image–for example, the car detection dataset had 720x1280 images–this step rescales the boxes so that they can be plotted on top of the original 720x1280 image.
def yolo_eval(yolo_outputs, image_shape = (720., 1280.), max_boxes=10, score_threshold=.6, iou_threshold=.5):
"""
Converts the output of YOLO encoding (a lot of boxes) to your predicted boxes along with their scores, box coordinates and classes.
Arguments:
yolo_outputs -- output of the encoding model (for image_shape of (608, 608, 3)), contains 4 tensors:
box_confidence: tensor of shape (None, 19, 19, 5, 1)
box_xy: tensor of shape (None, 19, 19, 5, 2)
box_wh: tensor of shape (None, 19, 19, 5, 2)
box_class_probs: tensor of shape (None, 19, 19, 5, 80)
image_shape -- tensor of shape (2,) containing the input shape, in this notebook we use (608., 608.) (has to be float32 dtype)
max_boxes -- integer, maximum number of predicted boxes you'd like
score_threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (None, ), predicted score for each box
boxes -- tensor of shape (None, 4), predicted box coordinates
classes -- tensor of shape (None,), predicted class for each box
"""
### START CODE HERE ###
# Retrieve outputs of the YOLO model (≈1 line)
box_confidence, box_xy, box_wh, box_class_probs = yolo_outputs
# Convert boxes to be ready for filtering functions (convert boxes box_xy and box_wh to corner coordinates)
boxes = yolo_boxes_to_corners(box_xy, box_wh)
# Use one of the functions you've implemented to perform Score-filtering with a threshold of score_threshold (≈1 line)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, score_threshold)
# Scale boxes back to original image shape.
boxes = scale_boxes(boxes, image_shape)
# Use one of the functions you've implemented to perform Non-max suppression with
# maximum number of boxes set to max_boxes and a threshold of iou_threshold (≈1 line)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes, max_boxes, iou_threshold)
### END CODE HERE ###
return scores, boxes, classes# Test
with tf.Session() as test_b:
yolo_outputs = (tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1))
scores, boxes, classes = yolo_eval(yolo_outputs)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
Pre-Trained YOLO
- Let’s use a pre-trained model and test it on the dataset.
- We’ll need a session to execute the computation graph and evaluate tensors
sess = K.get_session()Define Classes & Anchors
- Recall that we are trying to detect 80 classes, and are using 5 anchor boxes.
- We have gathered the information on the 80 classes and 5 boxes in two files “coco_classes.txt” and “yolo_anchors.txt”.
- We’ll read class names and anchors from text files.
- The car detection dataset has 720x1280 images, which we’ve pre-processed into 608x608 images.
class_names = read_classes("model_data/coco_classes.txt")
anchors = read_anchors("model_data/yolo_anchors.txt")
image_shape = (720., 1280.) Load Pre-Trained Model
- Training a YOLO model takes a very long time and requires a fairly large dataset of labelled bounding boxes for a large range of target classes.
- You are going to load an existing pre-trained Keras YOLO model stored in “yolo.h5”.
- These weights come from the official YOLO website, and were converted using a function written by Allan Zelener. References are at the end of this notebook. Technically, these are the parameters from the “YOLOv2” model, but we will simply refer to it as “YOLO”
# Load model from file which loads the weights of the trained model
yolo_model = load_model("model_data/yolo.h5")Summary
yolo_model.summary()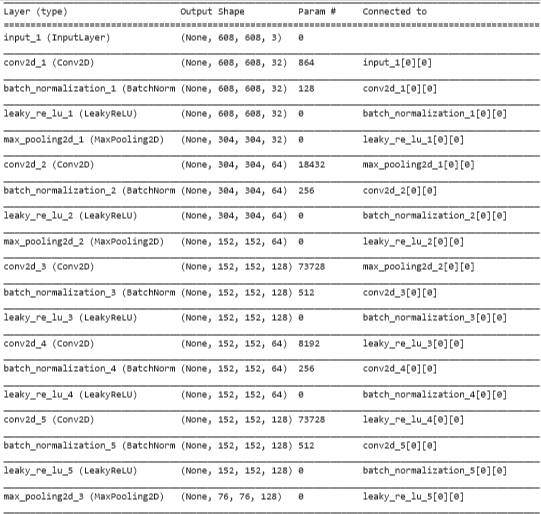
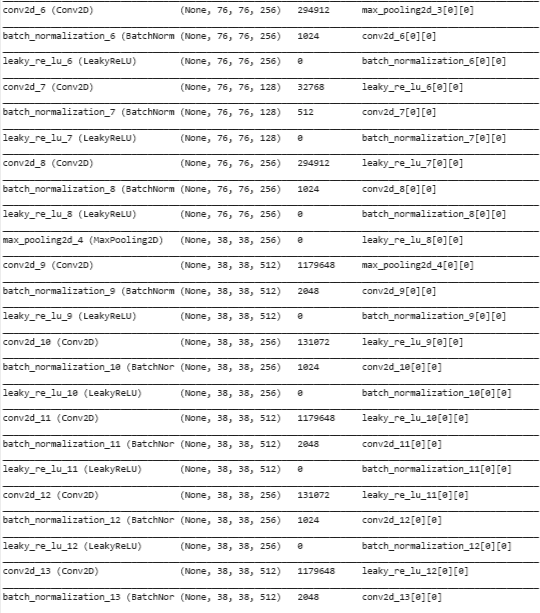
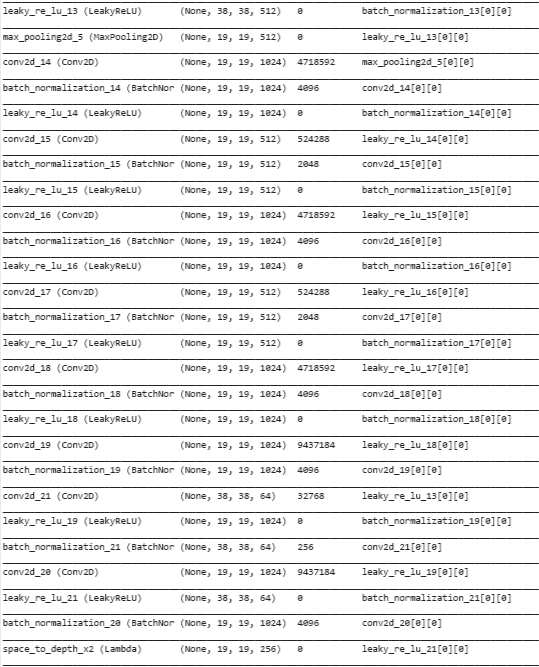

Convert to BB Tensors
The output of yolo_model is a (m, 19, 19, 5, 85) tensor that needs to pass through non-trivial processing and conversion. The following cell does that for you.
If you are curious about how yolo_head is implemented, you can find the function definition in the file ‘keras_yolo.py’. The file is located in your workspace in this path ‘yad2k/models/keras_yolo.py’.
yolo_outputs = yolo_head(yolo_model.output, anchors, len(class_names)) This set of 4 tensors is ready to be used as input by your yolo_eval function.
Filter
yolo_outputs gave you all the predicted boxes of yolo_model in the correct format. You’re now ready to perform filtering and select only the best boxes. Let’s now call yolo_eval, which you had previously implemented, to do this.
scores, boxes, classes = yolo_eval(yolo_outputs, image_shape)Graph on Image
So far we have:
- yolo_model.input is given to
yolo_model. The model is used to compute the output yolo_model.output - yolo_model.output is processed by
yolo_head. It gives you yolo_outputs - yolo_outputs goes through a filtering function,
yolo_eval. It outputs your predictions: scores, boxes, classes
Let’s create implement() which runs the graph to test YOLO on an image.
- image: a python (PIL) representation of your image used for drawing boxes. You won’t need to use it.
- image_data: a numpy-array representing the image. This will be the input to the CNN.
def predict(sess, image_file):
"""
Runs the graph stored in "sess" to predict boxes for "image_file". Prints and plots the predictions.
Arguments:
sess -- your tensorflow/Keras session containing the YOLO graph
image_file -- name of an image stored in the "images" folder.
Returns:
out_scores -- tensor of shape (None, ), scores of the predicted boxes
out_boxes -- tensor of shape (None, 4), coordinates of the predicted boxes
out_classes -- tensor of shape (None, ), class index of the predicted boxes
Note: "None" actually represents the number of predicted boxes, it varies between 0 and max_boxes.
"""
# Preprocess your image
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
# Run the session with the correct tensors and choose the correct placeholders in the feed_dict.
# You'll need to use feed_dict={yolo_model.input: ... , K.learning_phase(): 0})
out_scores, out_boxes, out_classes = sess.run([scores, boxes, classes], feed_dict={yolo_model.input: image_data, K.learning_phase(): 0})
# Print predictions info
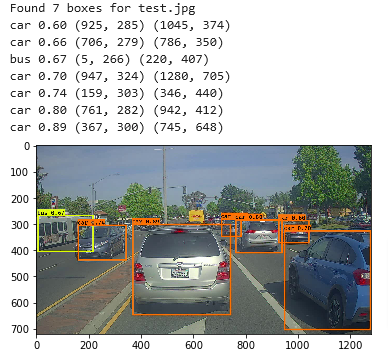
print('Found {} boxes for {}'.format(len(out_boxes), image_file))
# Generate colors for drawing bounding boxes.
colors = generate_colors(class_names)
# Draw bounding boxes on the image file
draw_boxes(image, out_scores, out_boxes, out_classes, class_names, colors)
# Save the predicted bounding box on the image
image.save(os.path.join("out", image_file), quality=90)
# Display the results in the notebook
output_image = scipy.misc.imread(os.path.join("out", image_file))
imshow(output_image)
return out_scores, out_boxes, out_classes# Test
out_scores, out_boxes, out_classes = predict(sess, "test.jpg")